Minimum Curvature
Minimum Curvature is widely used in the earth sciences. The interpolated surface generated by Minimum Curvature is analogous to a thin, linearly elastic plate passing through each of the data values with a minimum amount of bending. Minimum Curvature generates the smoothest possible surface while attempting to honor your data as closely as possible. Minimum Curvature is not an exact interpolator, however. This means that your data are not always honored exactly.
Minimum Curvature produces a grid by repeatedly applying an equation over the grid in an attempt to smooth the grid. Each pass over the grid is counted as one iteration. The grid node values are recalculated until successive changes in the values are less than the Maximum Residuals value, or the maximum number of iterations is reached (Maximum Iteration field).
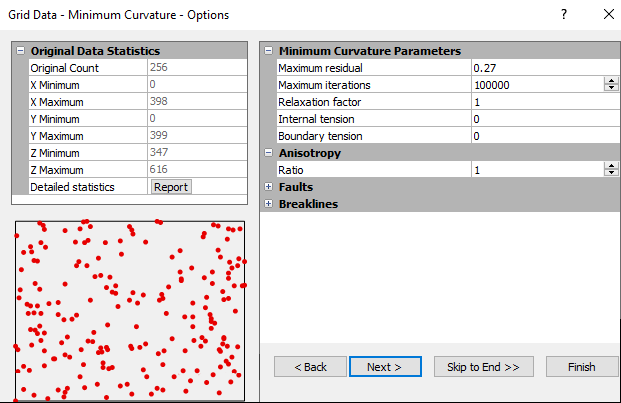
Minimum Curvature Options Dialog
In the Grid Data dialog, specify Minimum Curvature as the Gridding Method and click the Next button to open the Grid Data Minimum Curvature Options dialog.
|
|
|
Click the Advanced Options button in the Grid Data Minimum Curvature Options dialog to set the minimum curvature options. |
Maximum Residual
The Maximum Residual parameter has the same units as the data, and an appropriate value is approximately 10% of the data precision. If data values are measured to the nearest 1.0 units, the Maximum Residual value should be set at 0.1. The iterations continue until the maximum grid node correction for the entire iteration is less than the Maximum Residual value. The default Maximum Residual value is given by:
Default Max Residual = 0.001 (Zmax - Z min)
Maximum Iteration
The Maximum Iteration parameter should be set at one to two times the number of grid nodes generated in the grid file. For example, when generating a 50 by 50 grid using Minimum Curvature, the Maximum Iteration value should be set between 2,500 and 5,000.
Relaxation Factor
The Minimum Curvature gridding algorithm solves the specified partial differential equation using a successive over-relaxation algorithm. The interior is updated using a "chessboard" strategy, as discussed in Press, et al. (1988, p. 868). The only difference is that the biharmonic equation must have nine different "colors," rather than just black and white.
The Relaxation Factor is as described in Press et al. (1988). In general, the Relaxation Factor should not be altered. The default value (1.0) is a good generic value. Roughly, the higher the Relaxation Factor (closer to two) the faster the Minimum Curvature algorithm converges, but the more likely it will not converge at all. The lower the Relaxation Factor (closer to zero) the more likely the Minimum Curvature algorithm will converge, but the algorithm is slower. The optimal Relaxation Factor is derived through trial and error.
Internal and Boundary Tension
Qualitatively, the Minimum Curvature gridding algorithm is attempting to fit a piece of sheet metal through all of the observations without putting any creases or kinks in the surface. Between the fixed observation points, the sheet bows a bit.
The Internal Tension is used to control the amount of this bowing on the interior: the higher the tension, the less the bowing. For example, a high tension makes areas between observations look like facets of a gemstone.
The Boundary Tension controls the amount of bowing on the edges. The range of values for Internal Tension and Boundary Tension are 0 to 1.
By default, the Internal Tension and the Boundary Tension are set to 0.
Anisotropy
Set anisotropy settings if needed. For more information about anisotropy options, see Anisotropy.
Breaklines and Faults
Specify a breakline and/or fault. For more information, see Breaklines and Faults.