Radial Basis Function

Radial Basis Function interpolation is a diverse group of data interpolation methods. In terms of the ability to fit your data and to produce a smooth surface, the Multiquadric method is considered by many to be the best. All of the Radial Basis Function methods are exact interpolators, so they attempt to honor your data. You can introduce a shaping factor to all the methods in an attempt to produce a smoother surface. Regardless of the R² value, the Radial Basis Function is an exact interpolator.

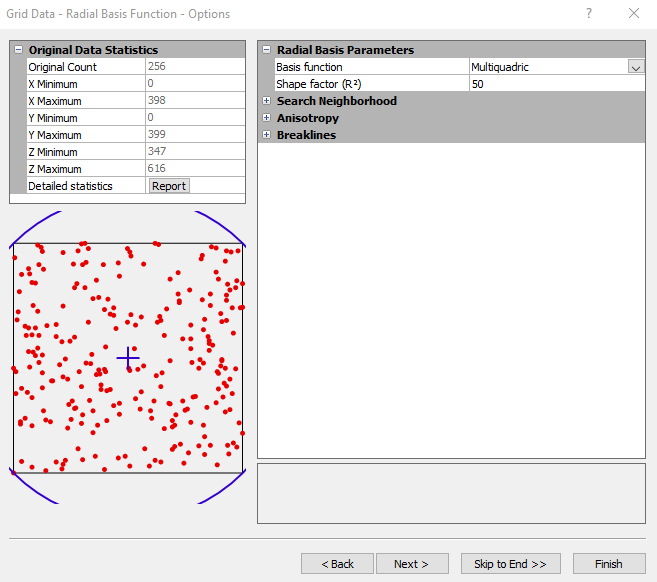
Radial Basis Function Options Dialog

In the Grid Data dialog, specify Radial Basis Function as the Gridding Method and click the Next button to open the Grid Data Radial Basis Function Options dialog.

Set the type of Basis Function and Anisotropy in the Grid Data Radial Basis Function Options dialog.

Basis Function

Specify the function type from the Basis Function list. The basis kernel functions are analogous to variograms in Kriging. The basis kernel functions define the optimal set of weights to apply to the data points when interpolating a grid node. The available basis kernel functions are listed in the Basis Function list in the Grid Data Radial Basis Function Options dialog.

Type	Equation
Inverse Multiquadric	$image\img00028.png$
Multilog	$image\img00029.png$
Multiquadric	$image\img00030.png$
Natural Cubic Spline	$image\img00031.png$
Thin Plate Spline	$image\img00032.png$

where:

h	= the anisotropically rescaled, relative distance from the point to the node
R²	= the shaping factor specified by the user

R² Parameter

The default value for R² in the Radial Basis Function gridding algorithm is calculated as follows:

(length of diagonal of the data extent)² / (25 * number of data points)

Search Neighborhood

Specify search rules. For more information about search rules, see Search.

Anisotropy

Set anisotropy settings if needed. For more information about anisotropy options, see Anisotropy.

Breaklines

The Breaklines section is used to add breaklines to the gridding process. Faults are not supported with Radial Basis Function.

References

A concise and readable introduction to Radial Basis Function interpolation can be found in Carlson and Foley (1991a). Given the clarity of presentation and the numerous examples, Hardy (1990) provides an excellent overview of the method, although this paper focuses exclusively on the special case of multiquadrics.

Carlson, R.E., and Foley, T.A. (1991a), Radial Basis Interpolation Methods on Track Data, Lawrence Livermore National Laboratory, UCRL-JC-1074238.

Carlson, R. E., and Foley, T. A. (1991b), The Parameter R2 in Multiquadric Interpolation, Computers Math. Applic, v. 21, n. 9, p. 29-42.

Franke, R. (1982), Scattered Data Interpolation: Test of Some Methods, Mathematics of Computations, v. 33, n. 157, p. 181-200.

Hardy, R. L. (1990), Theory and Applications of the Multiquadric-BiHarmonic Method, Computers Math. Applic, v. 19, n. 8/9, p. 163-208.

Powell, M.J.D. (1990), The Theory of Radial Basis Function Approximation in 1990, University of Cambridge Numerical Analysis Reports, DAMTP 1990/NA11.

Radial Basis Function