Modified Shepard's Method
Modified Shepard's Method uses an inverse distance weighted least squares method. As such, Modified Shepard's Method is similar to the Inverse Distance to a Power interpolator, but the use of local least squares eliminates or reduces the "bull's-eye" appearance of the generated contours. Modified Shepard's Method can be either an exact or a smoothing interpolator.
The Surfer algorithm implements Franke and Nielson's (1980) Modified Quadratic Shepard's Method with a full sector search as described in Renka (1988). (Surfer 6 was based upon Franke and Nielson, not Renka.)
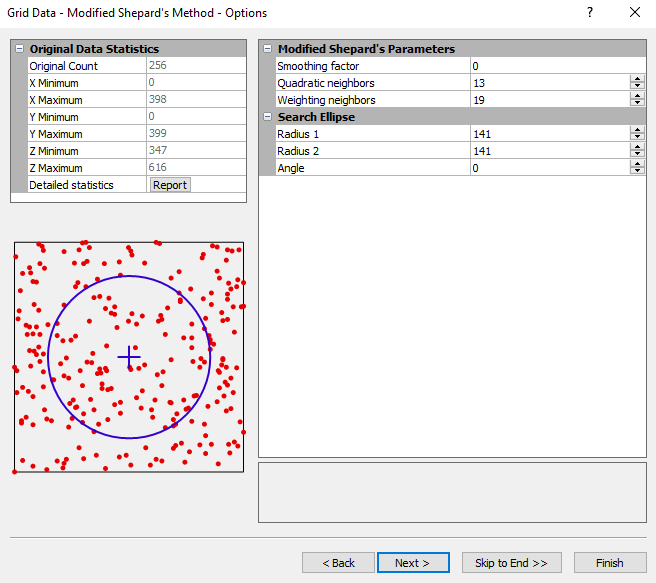
Modified Shepard's Method Options Dialog
In the Grid Data dialog, specify Modified Shepard's Method as the Gridding Method and click the Advanced Options button to open the Grid Data Modified Shepard's Method Options dialog.
|
|
|
Set the options, including search, and smoothing factor, in the Grid Data Modified Shepard's Method Options dialog. |
Smoothing Factor
You can assign a smoothing parameter to the gridding operation. The Smoothing Factor parameter allows Modified Shepard's Method to operate as a smoothing interpolator. Greater smoothing occurs as you increase the value of the smoothing parameter. In general, values between zero and one are most reasonable.
Quadratic Neighbors
The Modified Shepard's Method starts by computing a local least squares fit of a quadratic surface around each observation. The Quadratic Neighbors parameter specifies the size of the local neighborhood by specifying the number of local neighbors. The local neighborhood is a circle of sufficient radius to include exactly this many neighbors. The default value follows the recommendation of Renka (1988).
Weighting Neighbors
The interpolated values are generated using a distance-weighted average of the previously computed quadratic fits associated with neighboring observations. The Weighting Neighbors parameter specifies the size of the local neighborhood by specifying the number of local neighbors. The local neighborhood is a circle of sufficient radius to include exactly this many neighbors. The default value follows the recommendation of Renka (1988).
Search
You can set Search parameters in this dialog. For more information about search options, see Search.
References
Franke, R., and Nielson, G. (1980), 'Smooth Interpolation of Large Sets of Scattered Data', International Journal for Numerical Methods in Engineering, v. 15, p. 1691-1704.
Renka, R. J. (1988), 'Algorithm 660: QSHEP2D: Quadratic Shepard Method for Bivariate Interpolation of Scattered Data', ACM Transactions on Mathematical Software, v. 14, No. 2, p. 139-148.
Shepard, D. (1968), A two dimensional interpolation function for irregularly spaced data, Proc. 23rd Nat., p. 517-523.