Understanding Local Datums
To understand how local datum transforms affect data, you need to understand the ellipsoid, the spheroid, and how both relate to the datum. The spheroid is the a perfect circular object, located at mean sea level. This is constant everywhere. Because of local variations in the gravitational field, the shape actually has local variations.
|
|
|
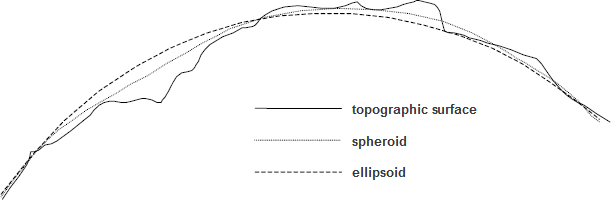
The image from Verhoogan, shows the variation in the geoid, ellipsoid, and actual topographic surface. |
The ellipsoid is used to approximate the global differences. But additional differences exist because of the actual topographic surface. Local datums were created to locally account for these differences. The datum includes the ellipsoid, the prime meridian shift, and any offsets in the X or Y direction. Because local datums align the ellipsoid with a particular location on the earth's surface, local datums are not suitable for use outside the designed area.
In the Define Coordinate System dialog, you can choose how datums are converted from one datum to another. This is the Conversion Method. The Molodensky method is the most widely used method of datum conversion. It adjusts latitude and longitude coordinates by taking into account the displacement between two datum's ellipsoids on all three axes. It does not take into account any rotational differences between the two ellipsoids. The Bursa-Wolfe method is similar to the Molodensky method, but in some instances it produces more accurate results because it takes into account both displacement and rotational differences between two ellipsoids. Surfer supports the Bursa-Wolfe method for conversions from the WGS84 datum to the following datums: World Geodetic System 1972, DHDN-1, DHDN, Australian Geodetic 1984, ANS84, MRT - Everest Modified, Switzerland - CH1903, NTF France - Paris Meridian, and Pulkovo 1942 - Hungary.
Changing the datum incorrectly can cause maps to appear wrong or not appear at all. It is advised that changing the datum be done with caution and a basic understanding of the local datums is advised.