Natural Neighbor
The Natural Neighbor gridding method interpolates grid values by weighting neighboring data points based on proportionate areas. Consider a set of Thiessen polygons (the dual of a Delaunay triangulation). If a new point (target) were added to the data set, these Thiessen polygons would be modified. In fact, some of the polygons would shrink in size, while none would increase in size. The area associated with the target's Thiessen polygon that was taken from an existing polygon is called the "borrowed area." The Natural Neighbor interpolation algorithm uses a weighted average of the neighboring observations, where the weights are proportional to the "borrowed area."
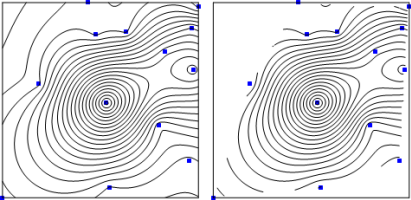
The Natural Neighbor method assigns the NoData value at and beyond the convex hull of the data locations (i.e. the outline of the Thiessen polygons).
|
|
|
The map on the left shows contours generated by the inverse distance to a power method. The map on the right shows contours generated by the natural neighbor method. Contours are not extrapolated beyond the boundary of the Thiessen polygons with the natural neighbor gridding method. |
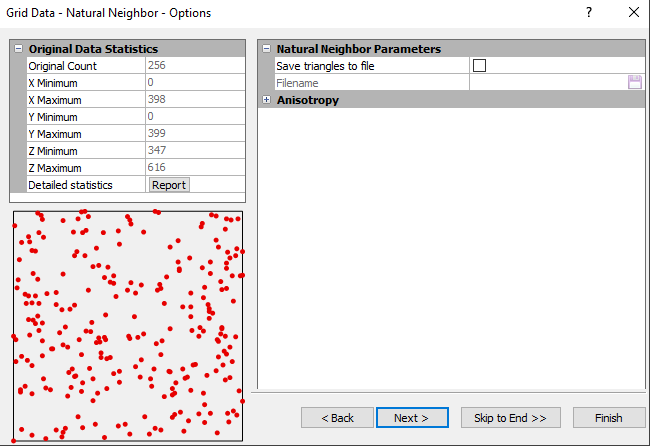
Natural Neighbor Advanced Options Dialog
In the Grid Data dialog, specify Natural Neighbor as the Gridding Method and click the Advanced Options button to open the Natural Neighbor Advanced Options dialog.
|
|
|
Set the anisotropy options and save Delaunay triangles in the Grid Data Natural Neighbor Options dialog. |
Save Triangles
Check the Save Triangles To box to export the Delaunay triangulation. The resulting file can be loaded as a base map and combined with other maps (i.e. contour maps, 3D surface maps, etc.).
Click the 
button to open the Export Triangles dialog. Specify a Save In location, File Name, and Save as type. The Delaunay triangle export formats include: .BLN, .BNA, .EMF, .GSB, .MIF, .PDF (Vector), and .WMF. Click the Save button to return to the Grid Data Advanced Options dialog.
Anisotropy
For more information about anisotropy options see Anisotropy.
References
The main reference for this method is Sibson (1981), however, also refer to Sibson (1980) and Watson (1994). Watson (1994) discusses the Natural Neighbor gridding technique in some detail, although Surfer does not use any of Watson's source code.
Sibson, R. (1980), 'A Vector Identity for the Dirichlet Tesselation', Math. Proc. Cambridge Phil. Soc., v. 87, p. 151-155.
Sibson, R. (1981), 'A Brief Description of Natural Neighbor Interpolation', Interpreting Multivariate Data, V. Barnett editor, John Wiley and Sons, New York, p. 21-36.
Watson, Dave (1994), Nngridr - An Implementation of Natural Neighbor Interpolation, David Watson, P.O. Box 734, Clarement, WA 6010, Australia.