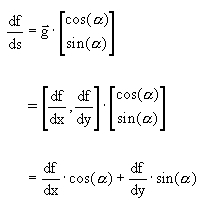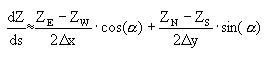First Derivative
The Grids | Calculate | Calculus directional derivative, First Derivative, calculates the slope of the surface along a given direction. First derivative grid files produce contour maps that show isolines of constant slope along lines of fixed direction. At a particular grid node location, if the slope is uphill, the slope is positive; and if downhill, the slope is negative. Slope is reported as rise over run and can approach negative or positive infinity as the slope approaches vertical in the down or up direction.
The directional first derivative is exactly as in the definition (Schwartz, 1974). Instead of a known function "Z(X,Y)" for which we can compute the necessary limits, Surfer uses a grid file, so directional derivative is approximated using difference equations.
|
|
|
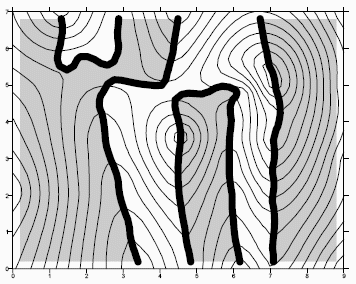
The original grid file is displayed as a contour map with thin contour lines. The first derivative map is overlaid on the contour map with negative values (downhill in the +x direction) in gray, positive values (uphill in the + x direction) in white, and the zero contour shown as a bold black line. |
The directional derivative at a point is equal to the dot product between the gradient vector and a unit vector in the direction of interest:
|
|
where a is the user specified angle (see Schwartz, 1974, p. 785, or Tuma, 1979, p. 89). Using compass-based grid notation, the equation takes the following form:
|
|