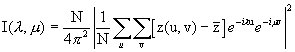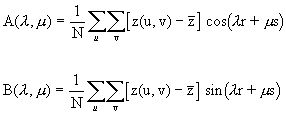Periodogram
The Grids | Calculate | Calculus Fourier and spectral analysis, Grid Periodogram, is a decomposition of the surface into the weighted sum of many two-dimensional sinusoids. This operation shows hidden periodicity or repeating patterns that might not otherwise be evident from looking at a contour map or surface.
Surfercomputes the grid periodogram for the two-dimensional Fourier frequencies. Grid periodograms have the same dimensions as the parent grids, but the axes represent the wave numbers associated with the Fourier frequencies. The grid periodogram surfaces are symmetric in the sense that Z(x, y) = Z(-x,- y).
In the current implementation of the grid periodogram there is no smoothing, no tapering, and no filtering. Such post-processing can be accomplished using the Grids | Calculate | Math capabilities.
|
|
|
A contour map of the function Z = sin ((x/5)-(y/7)) + cos((y/2)-(x/3)) is on the left, and the periodogram contour map is on the right. Due to symmetry, the four apparent peaks represent two peaks, one for each of the two fundamental sinusoids. |
Given gridded data z(u,v), where {u = 0, ..., NX-1} and {v = 0, ..., NY-1} the grid periodogram,
|
|
where 
.
The value of I(l,) is the weight or strength of the sinusoid with a two dimensional frequency of (,).
Breaking this calculation into the component real and imaginary parts yields:
|
|
Then
|
|
where
|
|
Surfer does not compute the grid periodogram, I(l,), for all possible frequencies (l,m) in this range. Rather, it computes the grid periodogram for the two-dimensionalFourier frequencies.
A two-dimensional frequency is a Fourier frequency if l is an integer multiple of 
, and m is an integer multiple of 
. In Surfer we consider the specific frequencies:
|
|
The indices (j, k) are called the wave number of the associated frequency (l,m). Surfer follows the engineering convention (rather than the mathematicians' convention) of plotting the grid periodogram as a function of the wave numbers rather than as a function of the frequency:
wave number = 2p / wavelength (e.g. radians/meter)
The maximum wave number is the Nyquist frequency =p/