Mathematical Functions

Mathematical Functions are used to modify data with the grid Function, Math, Grid Data, and Variogram commands in the plot window, and with the Transform command in the worksheet window.

Data Types

The expression evaluator supports 32-bit signed integer numbers, double-precision floating-point numbers, a boolean value, a text string of 0 to 256 characters, and time stamp values.

Variable Names

Variable names must begin with a column letter (i.e. A), row number (i.e. _1), or cell location (i.e. A2), which may be followed by other letters, numbers, or underscores (_), up to a maximum of 256 characters per variable name.

The variable names are not case sensitive. For example, sum(a..z), sum(A..z), and sum(A..Z) all refer to the same variable.

Precedence

The mathematical expression can consist of constants, variables (such as column letters), or functions (outlined below). The formulas follow standard precedence rules. Spaces are used in the equation for clarity.

Formulas are specified using standard precedence rules. Operators, in order of decreasing precedence, are:

(  )

parentheses

-

minus (or negative sign)

* /

multiplication and division

+ -

addition and subtraction

The expression evaluator treats operators with the following precedence:

  1. !, NOT, ~

  2. ^

  3. *, /, %

  4. +, -

  5. <<, >>

  6. <, >, <=, >=

  7. ==,!=,<>

  8. &

  9. XOR

  10. |

  11. &&, AND

  12. ||, OR

  13. ?:

  14. IF

Operators of equal precedence are evaluated from left to right within the equation. Parentheses are used to override precedence, and expressions with the parentheses are performed first.

The following built-in functions are supported.

Trigonometric Functions

All trigonometric functions are carried out in radians. If the data are in degrees, use the d2r(x) conversion function (in the Miscellaneous Functions section below) to convert degree data to radians and then use the trigonometric functions.

sin(x)

sine of angle x

cos(x)

cosine of angle x

tan(x)

tangent of angle x, the value of x must not be an odd multiple of /2

asin(x)

Arcsine in the range -/2 to /2, x must be between -1 and 1

acos(x)

Arccosine in the range 0 to , x must be between -1 and 1

atan(x)

Arctangent in the range -/2 to /2

atan2(y,x)

Arctangent of y/x in the range - to

Bessel Functions

j0(x)

j1(x)

jn(n,x)

Bessel functions of the first kind at x of orders 0, 1, and n, respectively

y0(x)

y1(x)

yn(n,x)

Return the Bessel functions of the second kind at x, of orders 0, 1, and n, respectively. For y0, y1, and yn, the value of x must not be negative.

Exponential Functions

exp(x)

exponential function of x (e to the x)

sinh(x)

hyperbolic sine of angle x

cosh(x)

hyperbolic cosine of angle x

tanh(x)

hyperbolic tangent of angle x

ln(x)

natural logarithm (base e) of x, x must be positive

log10(x)

base 10 logarithm of x, x must be positive

pow(x,y)

x raised to the yth power

Error conditions result if:

x is zero and y is negative or zero,

x is negative and y is not an integer,

an overflow results.

x^y

x raised to the yth power, see above

Miscellaneous Functions

min(x,y)

smaller of x and y

max(x,y)

larger of x and y

randn(x,y)

an approximately normally (Gaussian) distributed real random number with mean x and standard deviation y

randu(x)

a uniformly distributed real random number with mean of x from the interval [0,x]

row()

returns the row number

ceil(x)

next whole number greater than or equal to x

floor(x)

next whole number less than or equal to x

pi()

returns the value of Pi. To limit to a specific number of digits, use Round(Pi(),y) where Y is the number of digits after the decimal point

round(x, y)

X rounded to a the nearest number with Y digits after the decimal point

sqrt(x)

square root of x, x must not be negative

fabs(x)

absolute value of x

fmod(x,y)

floating point remainder of x/y, if y is zero, fmod returns zero

d2r(x)

convert angle x from degrees to radians. Example: sin(d2r(30)) computes the sine of 30 degrees. Sin(30) computes the sine of 30 radians

r2d(x)

convert angle x from radians to degrees

sign(x)

evaluate the sign of a number, returns -1 for x < 0, 0 for x = 0, and 1 for x>0

Statistical Functions of Intervals

sum(a..z)

calculates the sum of a range of columns in a row

sum(_1.._5)

calculates the sum of a range of rows in a column

avg(a..z)

calculates the average of a range of columns in a row

avg(_1.._5)

calculates the average of a range of rows in a column

std(a..z)

calculates the (population) standard deviation of a range of columns in a row

std(_1.._5)

calculates the population standard deviation of a range of rows in a column

rowmin(a..z)

finds the minimum value of a range of columns in a row

rowmin(_1.._5)

finds the minimum value of a range of rows in a column

rowmax(a..z)

finds the maximum value of a range of columns in a row

rowmax(_1.._5)

finds the maximum value of a range of rows in a column
  • The Statistical Functions of Intervals functions operate row-wise on an interval of columns or column-wise on an interval of rows.
  • The Statistical Functions of Intervals do not operate on cells. The equation B1 = avg(A1..A6) will result in only the average of row 1, not the average of the specified cells.
  • For example, SUM(A..Z) computes the sum of the twenty-six columns A, B, C, ..., Z. It does this for each row separately.
  • Replace 'a..z' by any valid interval of columns or rows, such as W..AC or _4.._612. There must be exactly two periods between the column or row labels. The labels may be given in reverse order, such as SUM(Z..A).
  • The Statistical Functions of Intervals functions can only be used in the worksheet. These functions cannot be used in Grid Math.

String Comparison

atof(x)

convert a string x to floating-point value

atoi(x)

convert a string x to an integer value

ftoa(x,y)

convert a floating-point number x to a string with y digits after the decimal point

strlen(x)

length of string x in characters

strcmp(x,y)

compare string x with y and return 1 if x>y, -1 if x<y, or 0 if x=y

stricmp(x,y)

compare string x with y without regard to the case of any letters in the strings

strncmp(x,y,z)

compare the first z characters of string x with y

strnicmp(x,y,z)

compare the first z characters of string x with y without regard to the case of any letters in the strings

String comparison functions work with strings, not numbers. Any rows or columns containing numbers result in blanks. In each of the string comparison functions, 1 is returned if string x is greater than string y, -1 is returned if string x is less than string y, and 0 if string x = string y. In the three-parameter comparison functions, the third parameter, z, specifies the number of characters to compare. For example, a z value of 3 compares the x and y strings' first three characters and ignores any characters after the third.

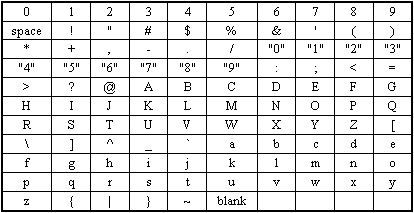
The comparisons are based on the standard ASCII table:

  1. numeric values (disregarded in string comparisons as mentioned above)

  2. cells starting with a space character

  3. common punctuation

  4. numeric text (numbers entered as text)

  5. less common punctuation

  6. uppercase letters

  7. even less common punctuation

  8. lower case letters

  9. uncommon punctuation

  10. blank cells (disregarded in string comparisons)

This is the ASCII table order. The table is read left to right, top to bottom. Items appearing toward the upper left corner are less than the items appearing toward the lower left corner.

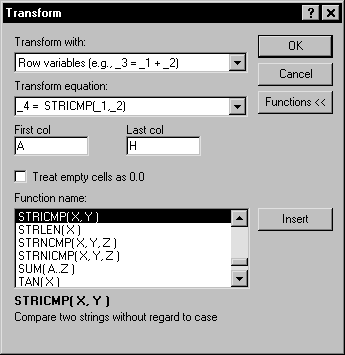
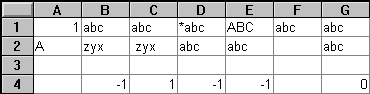
Example of a String Comparison

The following example shows a comparison of two strings in rows 1 and 2 with the results displayed in row 4. STRCMP returns a 1 if row 1 is greater than row 2; -1 if row 1 is less than row 2, and 0 if row 1 is equal to row 2.

This equation compares the strings in rows 1 and 2 and places the results in row 4.

This table includes results of the string comparisons based on the ASCII table. Cells containing numbers and blanks are ignored.

Boolean Expressions

Boolean expressions include:

  • Logical Operators (and, or, xor, not),

  • Comparison Operators (=, <>, <, >, <=, >=),

  • the IF Function - condition, true_value, false_value)

The words AND, OR, XOR, NOT, and IF are reserved keywords and may not be used as variable names.

Logical Operators (and, or, xor, not)

SYMBOL

NAME

DESCRIPTION

AND

AND

The result is true if both operands are true.

&&

AND

The result is true if both operands are true.

!

Logical NOT

Inverts the boolean value. True becomes false, false becomes true.

NOT

Logical NOT

Inverts the boolean value. True becomes false, false becomes true.

&

AND

The result is true if both operands are true.

|

OR

The result is true if either of the two operands is true

XOR

Exclusive-OR (XOR)

The result is true if both operands differ.

||

OR

The result is true if either of the two operands is true.

OR

OR

The result is true if either of the two operands is true.

Comparison Operators (=, <>, <, >, <=, >=)

SYMBOL

NAME

DESCRIPTION

~

Bitwise NOT

Inverts the bits in an integer

*

Multiply

Multiplies the two operands

/

Divide

Divides the first operand by the second

%

Remainder

Integer remainder of the first operand divided by the second

+

Add

Adds the two operands

-

Subtract

Subtracts the second operand from the first

<<

Shift Left

Shifts the operand to the left

>>

Shift Right

Shifts the operand to the right

<

Less Than

In the example, A1 < B1, the result is true if A1 is less than B1

<=

Less Than or Equal To

Result is true if the ordinal value of p1 is less than or equal to p2

>

Greater Than

Result is true if the ordinal value of p1 is greater than p2

>=

Greater Than or Equal To

Result is true if the ordinal value of p1 is greater than or equal to p2

==

Equal To

Result is true if the operands have identical values

!=

Not Equal To

Result is true if the operands do not have identical values

<>

Not Equal To

Result is true if the operands do not have identical values

IF Function - IF(condition, true, false)

SYMBOL

NAME

EXAMPLE

DESCRIPTION

IF

Conditional Evaluation

IF(p1,p2,p3)

IF(condition,true_value,false_value)

i.e. If p1 is true, the result will be p2. If p1 is false, the result will be p3.

IF

Conditional Evaluation

p1?p2:p3

condition?true_value:false_value

i.e. If p1 is true, the result will be p2. If p1 is false, the result will be p3.

NOTE: The return values must result in values with the same format (i.e. both text or both numeric). If needed, use the ftoa(x,y) function to convert a numeric value to text to conform with this requirement.

Examples

The following are examples of mathematical function syntax used in Surfer. With Grids | New Grid | Function and Grids | Calculate | Math use X,Y, and Z for the variables. If you use Data | Data | Transform in the worksheet, replace X,Y, and Z with column letters (A), row numbers (remember the underscore, _1 is row 1), or cell locations (A1).

Equation

Mathematical Function Syntax

x^2 or pow(x,2)

ln(x)

log10(x)

(1-exp(-X))

(1-exp(-X*X))

1-(sin(x)/x)

x^2/(1+x^2)

(2 * X) - X^2

( x^2+ y^2)*(sin(8*atan(x*y)))

See Also

Data Transform

Worksheet Error Codes and Special Numeric Values