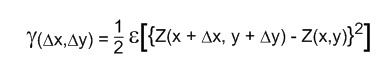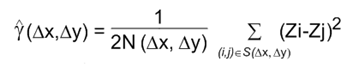What is a Variogram?
The mathematical definition of the variogram is
|
|
(3.1)
where Z(x,y) is the value of the variable of interest at location (x, y), and e[ ] is the statistical expectation operator. Note that the variogram, g( ), is a function of the separation between points (Dx,Dy), and not a function of the specific location (x, y). This mathematical definition is a useful abstraction, but not easy to apply to observed values.
Consider a set of n observed data: {(x1, y1, z1),(x2, y2, z2), … (xn, yn, zn)}, where (xi,yi) is the location of observation i, and zi is the associated observed value. There are n(n - 1)/2 unique pairs of observations. For each of these pairs we can calculate the associated separation vector:
(Dxi,j, Dyi,j) = (xi-xj, yi-yj)
(3.2)
When we want to infer the variogram for a particular separation vector, (Dx,Dy), we will use all of the data pairs whose separation vector is approximately equal to this separation of interest:
(Dxi,j, Dyi,j) » (Dx, Dy)
(3.3)
Let S(Dx,Dy) be the set of all such pairs:
S(Dx, Dy) = { (i,j) | (Dxi,j, Dyi,j) » (Dx, Dy) }
(3.4)
Furthermore, let N(Dx,Dy) equal the number of pairs in S(Dx,Dy). To infer the variogram from observed data we will then use the formula for the experimental variogram.
|
|
(3.5)
That is, the experimental variogram for a particular separation vector of interest is calculated by averaging one-half the difference squared of the z-values over all pairs of observations separated by approximately that vector.
Back to What Does a Variogram Represent?
Next to The Variogram Grid