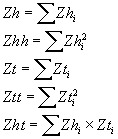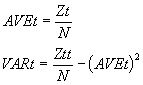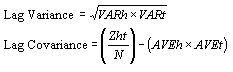Estimator Type
There are a number of different formulae for estimating the variogram. Each method has different strengths, weaknesses, and proponents. Surfer contains four estimating options: the variogram, standardized variogram, autocovariance, and autocorrelation. When in doubt use the default classical variogram.
An observation is an (X, Y, Z) triple. A pair of observations contains two such triples. Consider the set of N pairs of observations that go into the calculation of a single plotted point on an experimental variogram. These N pairs are ordered pairs; the two observations are not randomly ordered within a pair. The first observation in the pair is the point with the smaller Y value and the second observation is the point with the larger Y value. The first observation is called the "head" (denoted by an "h"), and the second observation is called the "tail" (denoted by a "t).
Let
be the observed value of the head observation of the ithpair, and
be the observed value of the tail observation of the ithpair.
The required sums over the set of all N pairs are denoted:
|
|
The average and variance for all of the observed head values are:
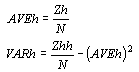
Similarly, the average and variance for all of the observed tail values are:
|
|
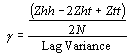
Then define the following two intermediate quantities:
|
|
Variogram
The "classical variogram" estimator is:
|
|
(seePannatier, 1996, p. 38).
Standardized Variogram
The standardized variogram estimator is:
|
|
(see Pannatier, 1996, p. 39).
Autocovariance
The autocovariance estimator is:
|
|
(see Pannatier, 1996, p. 41).
Autocorrelation
The autocorrelation estimator is:
|
|
(see Pannatier, 1996, p. 42).