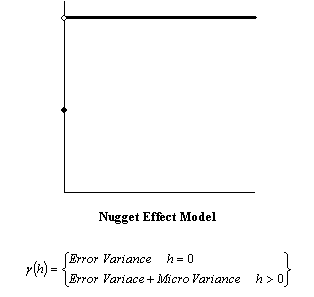
Nugget Effect
The Nugget Effect is used when there are potential errors in the collection of your data. The nugget effect is implied from the variogram you generate of your data. Specifying a nugget effect causes Kriging to become more of a smoothing interpolator, implying less confidence in individual data points versus the overall trend of the data. The higher the Nugget Effect, the smoother the resulting grid. The units of the nugget effect are the units of the observations squared.
The nugget effect is made up of two components:
Nugget Effect = Error Variance + Micro Variance.
Error Variance
The Error Variance is a measure of the direct repeatability of the data measurements. If you took an observation at one point, would the second measurement at that exact point be exactly the same as the first measurement? The Error Variance values take these variances in measurement into account. A non-zero Error Variance means that a particular observed value is not necessarily the exact value of the location. Consequently, Kriging tends to smooth the surface: it is not a perfect interpolator.
Micro Variance
The Micro Variance is a measure of variation that occurs at separation distances of less than the typical nearest neighbor sample spacing. For example, consider a nested variogram where both of the models are spherical. The range of one of the structures is 100 meters while the range of the second structure is five meters. If our closest sample spacing were 10 meters, we would not be able to see the second structure (five meter structure). The Micro Variance box allows you to specify the variance of the small-scale structure. If you do not know the micro variance, leave the setting at 0.0.
|
|
|
This is the nugget effect model. |
Reference
Surfer's implementation of the Nugget Effect follows the recommendation of Cressie (1991, Section 3.2.1), and this reference should be consulted for a more rigorous presentation of the nugget effect and its partitioning.